Pean tunnistama, et mulle lihtsalt meeldib matemaatika, meeldib samamoodi nagu kirjandus või muusika – mõtled tema peale ja seest läheb soojaks, näole tuleb naeratus. Seda tunnet on sama raske jagada nagu rõõmuvärinaid või kergust, mida võivad tekitada klaverimäng või sinilillevaip kevadises metsas.

Lihtsam on jagada tähelepanekuid ja mõttekesi – tervitusi matemaatikalt! Need tervitused tulevad seekord kolme pildina, kus lihtne ja keeruline on teineteisest sammu kaugusel ning nende eristamine õnnestub, kui üldsegi, vaid lähemal vaatlusel.

Aga olgem ausad, väike tagamõte või mure oli mul siiski ka. Ma vaatan enda ümber ja näen inimesi tulimeelselt arutlemas ja vaidlemas. Ja see on ju tore. Aga kui ma näen, kui enesekindlad ollakse oma argumentides ja mõttekäikudes, siis hakkab mul kõhe. Kujutan ette, et samasugust kõhedust võib tunda igaüks, kui ta näeb, et tema armsate töövahenditega – olgu neiks sõnad, viiulid või traktorid – käiakse ringi hooletult ja laisalt.

Kuulikestest

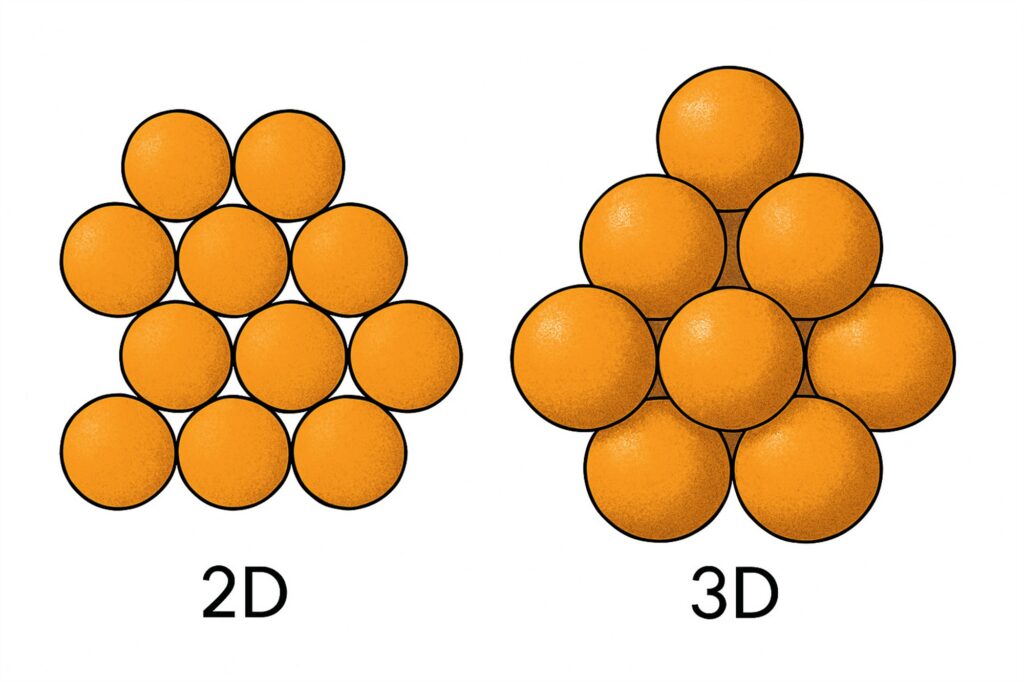
1611. aastal pakkus Johannes Kepler välja, et kahurikuulikesi on kõige optimaalsem laevale asetada joonisel toodud viisil. Näib loogiline? Tõestati see tulemus 1998. aastal Thomas Halesi poolt, kasutades arvuti abi. Tõestuse kontrollimine võttis ise veel kümmekond aastat.

Tuleb välja, et kuulikeste pakkimine ei ole ainult kahurifanaatikutele. Sama küsimus kõrgemates mõõtmetes (proovige ette kujutada kuule, palju kuule neljas, kümnes, kolmesajas mõõtmes!) omab rakendusi näiteks informatsiooni optimaalses edastamises. Võib ju ka informatsioonist lihtsustatult mõelda nagu teatud kuulikestest, mida tuleks optimaalselt paigutada, et neid läbi mürarikaste kanalite efektiivselt saata ja vastu võtta.

Millistes teistes mõõtmetes me sellisest kuulikeste pakkimisest aru saame?

Mõõtmetes 1 ja 2 on olukord klaar, näiteks kahes mõõtmes on küsimuseks ringide võimalikult tihe paigutus ja optimaalseks osutub just loomulik sümmeetriline paigutus (vt joonis 1). Mõõtmest kolm juba rääkisime. Mõõtmetest 4, 5, 6, 7 me matemaatiliselt aru ei saa … aga mõõtmes 8 on parim paigutus kindlaks tehtud ja selle eest sai 2022. aastal mu vahva kolleeg koduinstituudist (Lausanne’i föderaalne tehnoloogiainstituut, EPFL), ukrainlanna Maryna Viazovska matemaatikute kõrgeima auhinna, Fieldsi medali! Samamoodi lahendas ta ära ka ühe teise mõõtme – selleks oli 24. Kõikides muudes mõõtmetes on lahendus veel puudu. Kes osanuks seda aimata, et 8 ja 24 on lihtsamad kui 4, 5 ja 6 ? Kas pole veidi jahmatav?

Sellel on siiski ka matemaatiline, sügav matemaatiline selgitus – 8s ja 24s mõõtmes leidub eriliste sümmeetriatega võrestik, mis võimaldab optimaalset paigutust täpselt kirjeldada umbes samamoodi nagu kahes mõõtmes, kuigi seda ette kujutada ja kirjeldada on juba keerulisem, ning tõestada samuti. Selliste omadustega võret teistes mõõtmetes lihtsalt ei ole.

On see kõik siis lihtne, keeruline? Ja mis arvavad sellest kõigest kahurikuulid?

Arvudest ja võrranditest

Võrrandid on lihtsalt kompaktne viis kirja panna universaalseid suhteid eri suuruste vahel. Umbes nagu vend on hea ja kompaktne viis öelda meessoost isiku kohta, kes jagab sinuga ema ja isa. Näiteks võrrand x + 10 = y seab omavahel suhtesse arvud x ja y: arv y on kümne võrra suurem kui x. Igal võrrandil ei ole lahendit nagu mõnel inimesel pole venda; näiteks ei leidu kahte positiivset täisarvu, mille korral x^2 + y^2 = 3.

Tõesti, võib lihtsalt läbi proovida kõik arvud ja veenduda, et ükski arvupaar (x, y) ei rahulda antud tingimust. Tegelikult kõiki läbi proovida ei jõua, sest arve on lõpmatult palju, aga pole ka tarvis. Kui x = y = 1, siis x^2 + y^2 = 2 ja toodud suhe või võrrand ei kehti. Kui aga x = 2, siis on x^2 + y^2 juba vähemalt 4. Seega ei saagi see võrrand kunagi kehtida.

Vaatame nüüd kahte veidi keerulisemat võrrandit: 2x^6+3y^6 = z^6 ja x^6 + y^6 = z^6, kus x, y, z on positiivsed täisarvud. Leidub neile lahendeid? On ühte neist lihtsam lahendada kui teist?

Tuleb välja, et esimese võrrandi puhul võib paari minutiga veenduda, et lahendeid ei ole, teise jaoks läheb juba omajagu kauem, kuigi ta näeb ehk isegi lihtsam välja. Temaga sai ühele poole Leonhard Euler. Kuid kui astme 6 asemele võtta hoopis 5 ja kirjutada x^5+y^5=z^5, käis see Euleril üle jõu ja appi tulid järgmisest sajandi suurkujud Adrien-Marie Legendre ja Peter Gustav Lejeune Dirichlet. Kui aga võtta astmeks hoopis 59, oleks asi hoopis hull!

Nimelt alles 1995. aastal tõestas Andrew Wiles Fermat’ suure teoreemi, mis sai välja pakutud juba 1637. aastal ja mis väidab, et võrrandil x^n+y^n=z^n ei ole positiivsete täisarvude hulgas lahendeid niipea kui n on vähemalt 3. Uus Oxfordi matemaatikute maja sai selle tõestuse auks Andrew Wilesi nime ehk Andrew Wiles töötab Andrew Wilesi majas. Vähemalt see on vist lihtsus küll.

Perkolatsioon

Kolmanda näitena tooksin midagi oma uurimustööle lähedasemat. Perkolatsiooni mudel leiutati pärast Teist maailmasõda, et paremini mõista gaasimaske ja ehk parandada ka nende disaini. Hiljem on teda kasutatud ka teiste poorsete materjalide uurimiseks nagu näiteks maakihid, kust voolab läbi kõiksugu kasulikku ja kallist.

Mudeli lähtepunkt on lihtne: kujutame ette, et materjal koosneb miljonitest pooridest, mis on üksteisest sõltumatult teatava tõenäosusega p on kas lahti või kinni. Ehk siis iga avause jaoks viskame münti ja kui peale jääb kiri, mõtleme, et poor on lahti ja kui peale jääb kull, siis kinni. Münt ei pruugi olla aus – kiri jääb peale tõenäosusega p, mis võiks olla 1/2 aga näiteks ka 1/3 või 7/8.

Lihtsustuseks asetagem need poorid regulaarselt, ruutvõrestikku mööda kolmes mõõtmes (vt joonis 2). See oleks küll üks imelik kivi, aga matemaatiliseks alguspunktiks igati sobiv. Küsimus on nüüd järgnev – kui tõenäosus poori avamiseks on p, siis mis on tõenäosus, et kuubi ülaotsast sisse valatud vedelik jõuab alumisse otsa välja? Seesama p on nüüd ainus vaba parameteer, temast sõltub kõik.

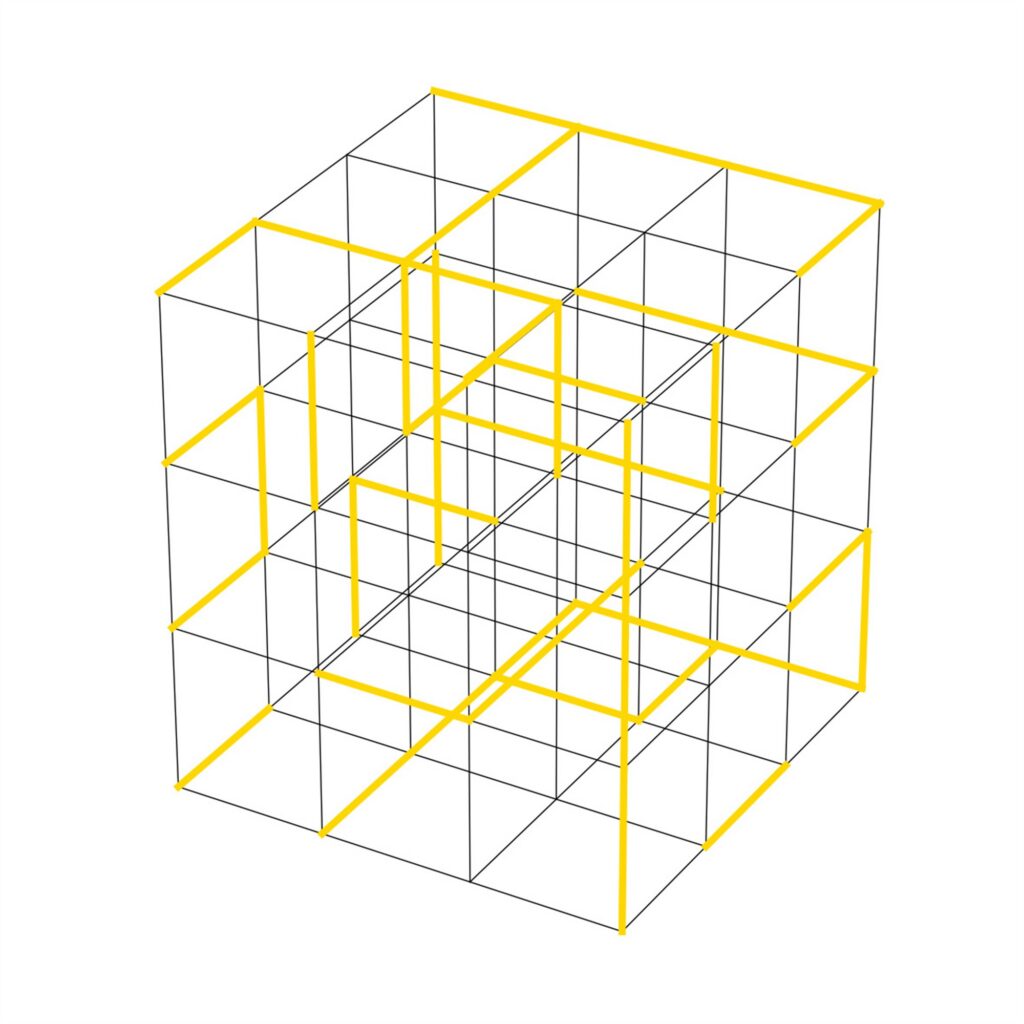
Tuleb välja, et see küsimus on üsna lihtne, kui p on peaaegu 1 – siis vedelik lausa kallab läbi – või kui p on peaaegu 0, siis ei tule pea tilkagi. Lisaks oleme aru saanud, et leidub üks p väärtus, kriitiline parameeter p_c, milllest kõrgemate p väärtuste jaoks vedelik pladiseb läbi ja alumiste jaoks vaevu tilgub. Matemaatiline ja kvantitatiivne arusaamine sellest fenomenist on kõvasti edenenud viimase kolmekümne aasta jooksul.

Aga me näiteks ei tea, mis see kriitilise parameetri p_c väärtus on! Ja me ei tea, mis juhtub täpselt sellel väärtusel. Oluliste edasiminekute eest perkolatsiooni ja sellega seotud küsimuste uurimises sai tore kolleeg Hugo Duminil-Copin Genfi ülikoolist samuti 2022. aastal Fieldsi medali. Jah, mulle meeldib mõelda, et matemaatikud jalutavad praegu lihtsa ja keerulise, juhuslikkuse ja struktuuri piirialadel.

Parameetri p väärtuse imeväike muutmine võib muuta süsteemi käitumist drastiliselt; ja sama drastiliselt võib parameetri p muutmine mõjutada, kas üks või teine matemaatiline argument nende uurimiseks töötab või ei. Kui ma annan teile p väärtuse 0,2588125, kas siis voolab vedelik läbi või ei? Aga kui väärtus on 0,2388125? Aga 0,2488125?

Detailid loevad ja usun, et mitte ainult matemaatikas.

On nagu on

Matemaatika on selline nagu ta on – ei lihtsam, ei keerulisem. Nagu Einstein olevat öelnud – kõik tehtagu nii lihtsaks kui võimalik, aga mitte lihtsamaks. Ma usun sellesse, usun lihtsusesse. Aga vahel on lihtsusel ja keerulisel keeruline vahet teha, isegi kui meil on silma ja kogemust. Arvad, et näpistad ühte, aga näppu jääb teine; ehitad ilusat argumendilossi, aga tuuleiil puhub pikali.

Kas ma ütlesin matemaatika? Võib-olla mõtlesin – maailm. Maailm on selline nagu ta on, lihtne või keeruline, ja tihti polegi selge, kui lihtne, kui keeruline.